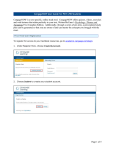
Download Athabasca University

Graphical Analysis for Windows
USER’S MANUAL
We should try another model. Click the Try New Fit
button and select the Inverse model from the Stock
Functions list. Again, the model does not provide a good
fit. The mean square error, 6280, is even larger. Click the
Try New Fit button and select the Exponential model.
This choice has provided a very good fit with a very small
mean square error, 0.453. If you click the OK - Keep Fit
button, you will return to the main screen.
The graph window will now look like the screen to the
left. The raw data will be graphed along with the
exponential model. A floating box will be displayed on
the graph. This box will contain the model, the calculated
coefficients, constants, and/or exponents, and the mean
square error.
17