1
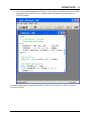
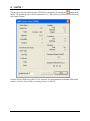
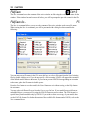
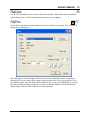
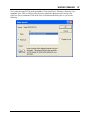
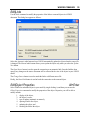
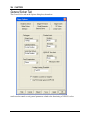
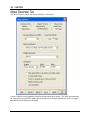
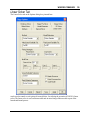
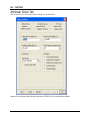
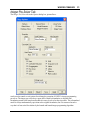
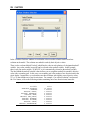
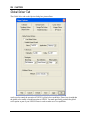
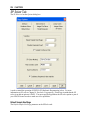
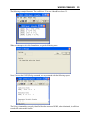
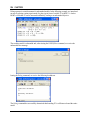
Download here in PDF
Transcript
520 CHAPTER 12 Logistics Models Capacitated Plant Location Model: CAPLOC Background The capacitated plant location model is a generalization of the transportation model we introduced in Chapter 1, Getting Started with LINGO. The capacitated plant location problem allows greater latitude of decision making in that the points of origin (plant locations) are variable. Manufacturers and wholesale businesses are likely to encounter problems of this sort in matching existing customer demand to product availability and minimizing transportation costs. The Problem in Words Your firm has a choice of three locations to operate a manufacturing facility in. Four customers exist with a known demand for your product. Each potential plant location has an associated monthly operating cost, and shipping routes to the demand cities have varying costs. In addition, each potential plant will have a shipping capacity that must not be exceeded. You need to determine what plant(s) to open and how much of a product to send from each open plant to each customer to minimize total shipping costs and fixed plant operating costs. The Model MODEL: ! Capacitated Plant Location Problem; SETS: PLANTS: FCOST, CAP, OPEN; CUSTOMERS: DEM; ARCS( PLANTS, CUSTOMERS) : COST, VOL; ENDSETS DATA: ! The plant, their fixed costs and capacity; PLANTS, FCOST, CAP = P1 91 39 P2 70 35 P3 24 31; ! Customers and their demands; CUSTOMERS, DEM = C1 15 C2 17 C3 22 C4 12; ! The plant to cust cost/unit shipment matrix; COST = 6 2 6 7 4 9 5 3 8 8 1 5; ENDDATA ! The objective; [TTL_COST] MIN = @SUM( ARCS: COST * VOL) + @SUM( PLANTS: FCOST * OPEN);
